Hiçbir ilke ya da kurama bağlı olmadan öğretim yapmak mümkündür ve muhtemelen ilkel toplumlarda öğretim böyle olmaktaydı. Belli bir plan ve ilkeler doğrultusunda yapılan eğitimin emek, zaman ve etkililik bakımından daha iyi olacağı açıktır. Matematik öğretiminde amaca ulaşılabilmesi için uyulması gerekli başlıca ilkeler aşağıda tanıtılmıştır.
Kavramsal temellerin oluşturulması: Matematik, kendisi başlı başına bir dil olduğu için birçok temel kavrama sahiptir. Kavram, sözcük olarak “belirli ortak özellikleri taşıyan nesne ve olayların adı” dır. Açı, üçgen, yüzey, işlem, benzerlik, limit, dizi, türev vs. birer matematik kavramdır. Bir matematik konusunun öğretimi yapılırken, o konuya ilişkin temel kavramları tam olarak kazandırmadan alıştırma ya da uygulama çalışmalarına geçmek ezbere öğrenmeye yol açar. Paralelkenar konusu incelenirken “paralelkenar nedir? Diğer dörtgenlerden farkı nedir?” Çokgensel bölgelerin alanları incelenirken “çokgen nedir? Alan nedir? Alanı ölçmek nedir?” sorularına verilen cevaplar kavram bilgisi ile ilgilidir. Bu sorulara tam cevap veremeden de öğrencilere, alan hesaplama formüllerini ezberlemek suretiyle, çokgensel bölgelerin alanları hesaplattırılabilir, ancak bu etkili ve kalıcı bir öğrenme olmaz.
Kavram bilgisini tam olarak verebilmek için öğretmenin dikkat edeceği nokta, konu ile ilgili tanımları tam olarak kazandırmaktır. Kavramın ne olduğunu vermenin yanı sıra ne olmadığının da verilmesi gerekir. Kavram kazandırılmadan alıştırmalara nadiren yer verildiği olur. Bu da kavrama karşı bir ilgi ve sempati oluşturmak için yapılır.
İlköğretimde kavram bilgisi verilirken fazlaca sembolik ve matematiksel dilden kaçınılmalı, öğrencilerin anlayabileceği bir dil kullanılmalıdır. Bir kavramın özellikleri, örnekleri değiştiği halde hep aynı kalan unsurlarıdır. Kavramın kazandırılmasında bunların öne çıkarılması önemlidir. Yamuk için “iki kenarı paralel olan düzlemsel dörtgendir” ifadesi gerekli ve yeterlidir. Bu tanımın verilmesi sırasında karenin, dikdörtgenin, paralelkenarın, eşkenar dörtgenin de birer yamuk oldukları ortaya konmalıdır. Bunlar yapılmadığı taktirde kavramla ilgili bilgi öğrencinin zihninde soyutlanmamış, netleşmemiş olur. Kavramların oluşturulması, kavramla ilgili detaylı bilgiye daha sonra yer verileceği durumlar (sözgelimi yamuğun çizimi, çevresi, alanı vs.) için çok önemlidir.
Önşartlılık ilişkisi: Matematik konuları diğer derslere göre daha güçlü bir sıralı yapıya sahiptir. Bunun temel nedeni matematiğin hiç bir dış katkı almadan kendisini üretmesidir, yani ardışık ve yığılmalı bir bilim olmasıdır. Herhangi bir kavram onun ön şartı durumundaki diğer kavramlar kazandırılmadan tam olarak verilemez.
Önşartlılık ilişkisi bazı konular için doğrusal bir yapıdadır.
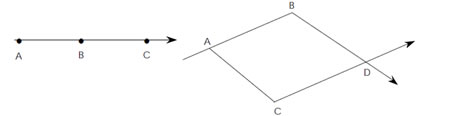
Şekildeki A kavranmadan B’ye, B kavranmadan C’ye geçme şansı yoktur. Sayıların öğretimi bu modele uygundur. Tek basamaklı sayılar öğrenilmeden iki basamaklılar, iki basamaklılar öğrenilmeden üç basamaklılar öğrenilemez. Bu durum tüm konularda ortaya çıkmaz. Bazı konularda temel alınacak konu çeşitlilik gösterebilir. Bunu şöyle örnekleyebiliriz. Üçgenin alanını kavratmak için dikdörtgenin alanından yararlanılabileceği gibi paralelkenarın alanından da yararlanılabilir. Bu modele ağ modeli denilebilir. Ağ modelinin uygun düştüğü konularda öğretmen, temel alınacak konulardan hangisi sınıf tarafından daha iyi biliniyorsa konuyu onun üzerine kurmalı ve ondan yararlanmalıdır. Önşartlılık ilişkisi olan konuların her birinin bilinmesi halinde, bunlardan birine öğretim sırasında yer vermek, diğerini uygulama sırasında kullanmak ve böylece öğrencilere seçenek sunmak en idealidir.
Anahtar kavramlara önem verme: Bazı matematik kavramlar, diğer konuları işlerken bir araç gibi kullanılır. Bunlara bilgiyi hatırlama veya üretme için sıkça başvurulur. Birim çember, kenarları 2 birim olan eşkenar üçgen, dikkenarları 1’er birim olan ikizkenar dik üçgen, açıların trigonometrik değerlerini bulmada birer araçtırlar. Sayı doğrusu, işlem tekniğinin ve sayı sisteminin kavratılmasında, sık kullanılan bir araçtır.
İşlemlerin özellikleri, zihinden hesap yapmanın anahtarıdır. Bu yüzden öğrenildiği gibi kalmamalı, gerek günlük hayatımızda, gerekse derslerin kapsamındaki hesaplamada kullanılmalıdır. Burada öğretmene düşen görev, araç niteliğindeki bu kavramları kendisinin kullanması ve yeri geldiğinde de öğrencilere kullandırtmasıdır.
Öğretimde öğretmen ve öğrencinin görevlerinin iyi belirlenmesi: Matematik derslerinde öğretmen, yeri geldikçe konuyu açıklayarak anlatan, yeri geldikçe öğrencilerle tartışan, yeri geldikçe sadece öğrenci çalışmalarını izleyen konumlardadır.
Mutlaka öğretmen tarafından anlatılması ve açıklanması gereken “örneğin; iki kesrin birbiriyle çarpılması, trigonometrik denklem, eşitsizlik vb.” soyut kavramların verildiği durumlarda öğretmene büyük görev düşer. Eğer öğretmen, öğretimi amaçları doğrultusunda gerçekleştiremezse, öğrencilerde ezberleme eğilimi artar veya onarılması güç hatalı öğrenmeler ortaya çıkar. Bunun yanısıra matematik derslerinin büyük bir çoğunluğunda öğretmen sınıfta araç ve materyal hazırlığı yapan, öğrencilerin grup şeklinde mi yoksa bireysel olarak mı çalışacağına karar veren, onların bilgiyi üretmeleri ve kullanmaları için ortam hazırlayan bir kişidir. Bu ortamı hazırladıktan sonraki görevi, öğrencilerin bilgiyi üretme ve uygulama sırasında çektikleri güçlükleri gözlemek ve onlara yardımcı olmaktır. Çalışma sonunda ise, sınıf tartışması açıp konu ile ilgili ortak sonucu öğrencilerle paylaşmak ve öğrencilerin birbirleriyle paylaşmasını sağlamaktır.
Öğretimde çevreden yararlanma: Matematik öğrenmenin temel amacı çevreden ve olaylardan anlam çıkarma, onları daha iyi yorumlayabilme olup, bu amaca en iyi şekilde ulaşabilmek için, bazen çevre sınıfa, bazen de ders çevreye taşınmalıdır. Böylece öğrenilen bilgi, daha kolay uygulamaya geçirilebilir. Bu durum özellikle ilköğretim matematiği için çok önemlidir ve ilköğretim matematiğinin her konusu için uygun örnekler vardır. Çokgensel bölgelerin alanlarının hesaplanmasında “evimizin ya da sınıfımızın pencere camı tutarının, boya-badana tutarının hesaplanması”, yüzde (%) hesaplarının öğretiminde bir banka hesap defterindeki işlemlerin analizi, hacim hesaplarında bir marketten alınan farklı boylardaki kutu ambalajlar üzerinde çalışma, grafiklerin öğretimi için, altın ve döviz fiyatlarındaki değişimi gösteren gazete sayfaları, alışveriş hesapları için bir lokantanın yemek fiyat listesi veya marketlerin fiyat cetvelleri uygun araçlardır.
Araştırma çalışmalarına yer verme: İlköğretim matematiği öğretim etkinliklerinde, öğrencilerin düzeylerine uygun olarak, rutin olmayan problemler ve araştırma çalışmalarına yer verilmeli, onların bu konular üzerinde bireysel ya da grupça çalışmaları sağlanmalıdır. Bu tür çalışmalar onların öğrendiklerini uygulamalarına olanak sağladığı gibi bağımsız çalışma, özgün düşünme ve açıklama yapma yeteneklerini geliştirir. Örneğin; “Kenar uzunlukları 60 cm ve 100 cm olan dikdörtgen şeklindeki bir kartondan en
büyük hacimli üstü açık kutu yapabilmek için köşelerden kesilmesi gereken karelerin boyutu ne olmalıdır?” Böyle bir çalışma öğrencilerin yürütebileceği bir araştırmadır (Bu problemin kesin cevabı, üst düzey bir kavram olan türev kavramını gerektirir). Bu düzeyde beklenen ise, öğrencilerin köşelerden kesilen karenin boyutunun değişimi ile oluşan kutunun hacminin değişiminin paralellik göstermediği, ancak en büyük olan bir hacim değerin varlığını fark etmeleri ve bunu bulmaya çalışmalarıdır. Bu amaçla öğrencilerin aşağıdaki tabloyu doldurmaları ve bu tablonun satırlarını ihtiyaca göre artırmaları gerekli ve yeterlidir.
Matematiğe karşı olumlu tutum geliştirme: Öğrencilerin birçoğu hata yapma korkusuyla matematik etkinliklerinden uzak durmakta ve başarısız olmaktadır. Matematik korkusu ve kaygısı üzerine yapılmış araştırmalar öğrencilerin matematikle ilgili yaşantıları arttıkça, matematiğe karşı olumlu tutumlarında azalmalar gözlendiğini ortaya koymuştur. Öğrencinin matematiğe karşı tutumunda, öğretmenin rolü büyüktür. Bu nedenle öğretmen, öğrencilerin matematiğe karşı olumlu tutum geliştirmelerini sağlayacak önlemler almalıdır.
Önerilen bazı önlemler şunlardır:
· İlkokulun ilk yıllarından itibaren öğrenciler gelişmişlik düzeylerine uygun matematik etkinliklerle karşı karşıya getirilmeli, onların kapasitelerini zorlayacak etkinliklerden kaçınılmalıdır.
Matematik derslerinde uzun ve can sıkıcı ödevlerden kaçınılmalı, alışılmış rutin alıştırmaların yanısıra öğrencilerin ölçme yapmalarını gerektiren, onları araştırmalara yönelten ödevler de verilmelidir.
İşlem kavramları ve bu işlemlerin teknikleri öğretilirken ezberleme yerine bunların anlamları üzerinde durulmalı, işlemlerin tekniklerini açıklayıcı ders materyali, kavram ve algoritmalar pekişinceye kadar öğrencilerin görebilecekleri mekanlarda bulundurulmalıdır.
Öğretmen, matematikte aynı sonuca ulaşan yöntemlerin çokluğunu sezdirmeli ve öğrencilerin bulduğu farklı çözümleri önemsemelidir.
Çocuklar gerek işlem ve çizim yaparken, gerek problem çözerken yeterli zaman kullanabilmeli, yetiştirememe kaygısı içinde bırakılmamalıdırlar. Ayrıca öğrencilerin problem çözme ve işlem yapma sırasında düştükleri hatalar hoşgörü ile karşılanmalı, bu hataları giderici, onarıcı ve yol gösterici çalışmalar yapılmalıdır.
Matematiğin eğlendirici, dinlendirici yanı öğrencilere tanıtılmalı, matematik öğretiminde oyunlaştırılmış etkinliklere yer verilmelidir.
Matematik etkinlikler sırasında öğrencilerin kendi düşüncelerini açıklamaları için fırsatlar verilmeli, başarılı öğrencilerin hızlı çözümlerinin, yavaş olan öğrencileri bloke etmesi önlenmelidir.
Kaynak:Prof. Dr. Hüseyin Alkan, Yrd. Doç. Dr. Murat Altun; Editör: Prof. Dr. Aynur Özdaş, “Matematik Öğretimi”, Matematik Öğretmenliği, T.C. Anadolu Üniversitesi Yayınları No: 1072, Açıköğretim Fakültesi Yayınları No: 591, ISBN 975 – 492 – 825 – 8, 1998.



