Matematiği somut ve soyut oluşuna göre ikiye ayırmak mümkündür. Somut matematik, pratik hesaplamalar, problem çözme ve ölçme yaparken kullandığımız matematiktir. Buna faydacıl ya da sosyal değer taşıyan matematik diyebiliriz. İkincisi, matematiğin kendi iç tartışmalarının yer aldığı matematiktir. Teoremlerin ispatı, sayı sistemlerinin kurulması, yeni matematik yapıların oluşturulması ve bunların iç dinamiğinin açıklanması bu kapsamdadır. Bu tür matematik pür matematik diye bilinir ve soyuttur. Pür matematiğin hayatla ilişkisi zaman içinde oluşmaktadır. Gelişmesi sadece insan zihninin merakını giderme ve gerçeği bulma uğraşına bağlıdır.
Matematiğe değişik cephelerden bakıldığında bazı sınıflamalar yapmak mümkün olur. Matematiği değişik cephelerden gösteren Şekil 1’deki prizmadan, kapsamındaki alanlar itibariyle matematiğin, sayılar, cebir, ölçüler, şekiller ve cisimler ve veri işleme (istatistik) olmak üzere beş temel alana ayrıldığı görülür.
Matematiğe uygulama alanları cephesinden baktığımızda üç ayrı uygulama alanı görebiliriz. Bunlar;
- Pratik etkinlikler,
- Gerçek hayat etkinlikleri
- Matematiğin kendi iç tartışmaları.
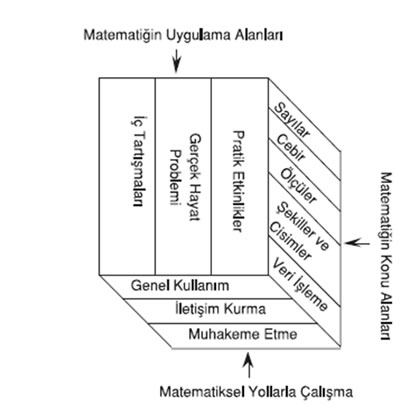
Matematiği; bilgi ve beceri kazanma amacıyla, günlük işleri yürütmede kullanma, pratik etkinlikler kapsamında, bir köprü yapımında ya da bir direğin boyunu hesaplama amacıyla kullanma gerçek hayat problemleri kapsamında, teoremlerin ispatı, cebirsel yapılar oluşturma ve matematik problemlerinin çözümü için kullanma matematiğin kendi iç tartışmaları kapsamında düşünülen etkinliklere örnek olarak gösterilebilir.
Matematiksel yollarla çalışma (Matematiğin hayatı etkileyiş biçimi) cephesinden baktığımızda da matematiği üç ana bölüm halinde ele alabiliriz. Bunlar
- Genel kullanım,
- Matematik ile iletişim,
- Muhakeme etmedir.
Genel kullanım kapsamında; bir işi yaparken ihtiyaç duyulan matematiği kullanma, matematiği kullanarak bir işi planlama, elde edilen sonuçların gerçeğe uygunluğunu test etme, problemlere değişik çözümler sunmayı düşünebiliriz. İletişim kurma kapsamında; matematik bilgiyi anlama ve yorumlama, bir işle ilgili mantık yürütme, bir soru üstüne konuşurken matematikten yararlanma, bir çözümün sonuçlarını anlamlı biçimde sunma. Son olarak muhakeme etme kapsamında da; hipotez kurma ve genelleme yapma, tahmin etme, ispat yapma, ispatı reddetme, tanım yapma, verilere bakarak sezgide bulunma gibi etkinlikleri sayabiliriz.
Kaynak:Prof. Dr. Hüseyin Alkan, Yrd. Doç. Dr. Murat Altun; Editör: Prof. Dr. Aynur Özdaş, “Matematik Öğretimi”, Matematik Öğretmenliği, T.C. Anadolu Üniversitesi Yayınları No: 1072, Açıköğretim Fakültesi Yayınları No: 591, ISBN 975 – 492 – 825 – 8, 1998.



